An Automatic Baseline Correction Method for Raman Spectra

With a few lines of code, we can easily batch subtract spectral background.

In this post:

An algorithm based on asymmetric least squares (ALS) smoothing
Python code implementation

Credit: Dr Tabitha Jones, my colleague who supervised me a lot not just this portion, currently is Research Associate at University of Cambridge.

Fluorescence in Raman Spectroscopy

The signal in Raman spectroscopy has three components: vibrational bands, noise, and fluorescence. Fluorescence occurs when a photon of the incoming radiation is absorbed by an orbital electron in a molecule of the material, exciting it to a higher energy level. The practical consequence of this in Raman spectroscopy is that intense fluorescence emissions from a sample can obscure weaker vibrational fingerprints and reduce the quality of spectra. Thus, it is necessary to remove the baseline drift in spectroscopic analysis.

Background subtraction is a crucial step in the preprocessing of Raman spectra, it can be implemented by either manual or automation means in professional plotting software (e.g. Origin). However, these approaches are usually subjective, time-consuming and of limited reproducibility, and a highly compelling alternative is algorithm-based automated signal processing.

ALS Baseline Correction

Asymmetric Least Squares (ALS) is a growing baseline estimation method, developed by Eiler¹, that uses an asymmetric weighting of deviations to smooth data and estimate a baseline, extending ideas presented by Whittaker 80 years ago. This smoother is simple and fast, allowing to be programmed in a few lines of code.

Specially, it refers to the algorithm based on searching a smooth line (\(z\)) lower than the experimental data (\(y\)) by penalizing the second derivative of the former. Mathematically, it is briefly expressed as the following functional:
\[ F=\sum_{i}w_i(y_i-z_i)^2+\lambda\sum_{i}(z_i'')^2\notag \]

where the summation runs over all points of the x-axis, \(w_i\) is chosen asymmetrically: \(w_i = p\) if \(y_i > z_i\) and \(w_i=1-p\) otherwise, and \(\lambda\) is the penalty parameter for the second derivative. In a nutshell, this method can: Quickly correct and ascertain a baseline and Retain signal peak information.

Implementation & Application

Based on the algorithm, Python Scipy package is called to defined the corresponding function, which then can be used for raw spectral data ergodic extraction and batch processing.

import numpy as np
from scipy.sparse import csc_matrix
from scipy.sparse import spdiags
from scipy.sparse.linalg import spsolve

def ALSBaselineCorrection(y, lam=1E6, p=0.001, niter=30):
    m = len(y)
    w = np.ones(m)
    D = csc_matrix(np.diff(np.eye(m), 3))
    for i in range(niter):
        W = spdiags(w, 0, m, m)
        Z = W + lam * D.dot(D.transpose())
        z = spsolve(Z, w * y)
        w = p * (y > z) + (1 - p) * (y < z)
    return z

Here is an example of my own experimental data. In Surface Enhanced Raman Scattering (SERS) sensing of adenine, a purine nucleotide base, high fluorescence exhibits due to the presence of graphene oxide in the measurement system. As can be seen, after ALS smoothing, the drifting baseline is pulled back to zero intensity, and almost all the Raman signals are well preserved.

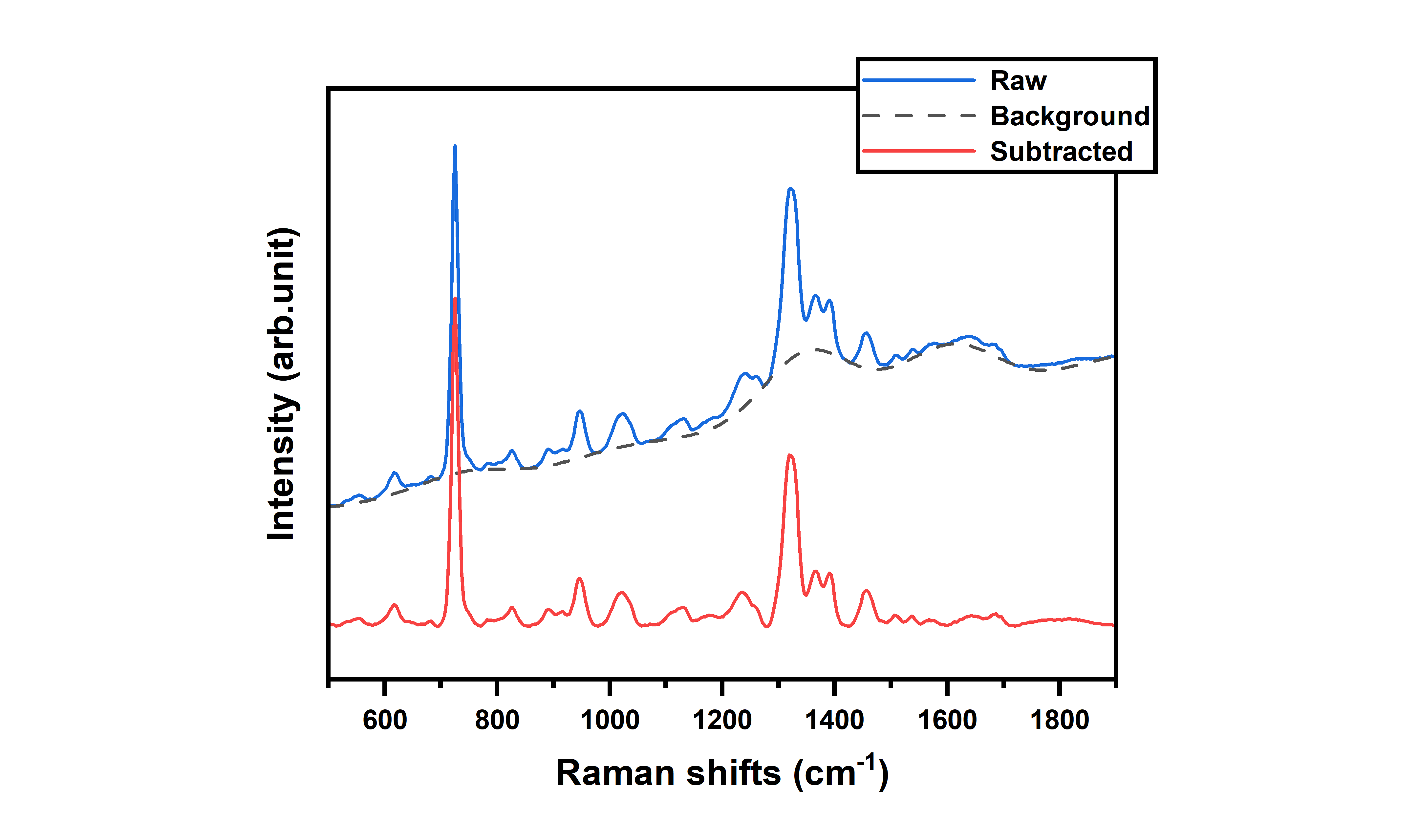
Surface Enhanced Raman Spectrum of Adenine Before/After Baseline Correction